Note: This lesson and Lesson 6-I are really two parts of one whole. It's advisable to either do them at the same time, or to do Lesson 6-II very shortly after completing Lesson 6-I.

In Lesson 6-I, we considered the problem of saving money at a fixed interest rate, compounded, with regular deposits. Now we're going to turn that around. What if, instead of the bank paying you money, you owed they bank money (perhaps, sadly, a more common occurrence these days)? Instead of making regular deposits to save up, we'll discuss making regular payments toward the balance of the loan.

It turns out that the mathematics of the situation are roughly the same.

Along the way, we'll learn about the time value of money and compound interest. What should our monthly payments be in order to pay the loan off after a certain number of months?

The Mathematical Model

The word equation looks quite similar to the word equation for an interest-bearing deposit account:

$[balance\ this\ month]=[balance\ last\ month]+[interest\ on\ last\ month's\ balance]-[payments\ this\ month]$

The interest on last month's balance is

$[interest\ on\ last\ month's\ balance]=[balance\ last\ month]\times\frac{[annual\ interest\ rate]}{12}$

Let's use the following symbols (which are somewhat standard):

variable/parameter	interpretation	units
$t$	time	months
$y_t$	balance (amount owed)	$
$P$	monthly payment	$
$I$	annual interest rate

Just as we did in Lesson 5-I, we obtain the finite difference model:

$y_t=y_{t-1}+y_{t-1}\cdot\frac{I}{12}-P$

or in "simplified" form

$y_t=\left(1+\frac{I}{12}\right)y_{t-1}-P$

The only difference between this equation and the one in Lesson 6-I is the sign. We have "-P" because each regular payment reduces our balance owed; in Lesson 6-I each regular payment increased the balance we had in our account so we wrote "+D".

Since we are looking at essentially the same equation, we can solve it the same way. Recall there are two methods to be used with a finite difference model: iteration (which involves arithmetic, so Excel is the appropriate tool) and algebra (for which Maple is best).

The Implementation: Iteration (Excel)

Let's see what happens if we start off owing an initial debt of $10,000, at a rate of 6%, and we make monthly payments of $150.

As before, we'll make a table of values labeled t and y. Also we'll make a parameter table to make it easier to see the effects of changing interest rate and monthly payments. In cell B2, enter 10000 for the initial balance of the debt, and in cell B3, use the parameter values to enter the Excelified version of the formula above in cell B3.

As usual, we use $s in the formula whenever we reference cells where parameters are stored. Now, as in Lesson 5-I, copy-and-paste the formula down column B until we get to our goal -- which, this being a debt, is to have a balance of $0. Here that looks to be after about 82 months.

The Implementation: Algebra (Maple)

Let's say the $150 monthly payment we're making is the minimum monthly payment that our credit card company insists we make.

When, precisely, will the debt be paid off?
If we want to pay off the debt in two years (24 months), what monthly payment should we make?

Instead of plugging in numbers and iterating, we'll just do it with symbols. That is, we'll do algebra instead of arithmetic.

The key algebraic observation is that we can combine the equations

$y_2=\left(1+\frac{I}{12}\right)y_1-P$

and

$y_1=\left(1+\frac{I}{12}\right)y_0-P$

to obtain:

$y_2=\left(1+\frac{I}{12}\right)\left[\left(1+\frac{I}{12}\right)y_0-P\right]-P$

which can in turn be simplified to:

$y_2=\left(1+\frac{I}{12}\right)^2y_0+\left[1+\left(1+\frac{I}{12}\right)\right](-P)$

We can then plug this into the equation

$y_3=\left(1+\frac{I}{12}\right)y_2-P$

to obtain

$y_3=\left(1+\frac{I}{12}\right)^3y_0+\left[1+\left(1+\frac{I}{12}\right)+\left(1+\frac{I}{12}\right)^2\right](-P)$

and similarly

$y_4=\left(1+\frac{I}{12}\right)^4y_0+\left[1+\left(1+\frac{I}{12}\right)+\left(1+\frac{I}{12}\right)^2+\left(1+\frac{I}{12}\right)^3\right](-P)$

The pattern continues like this:

$y_t=\left(1+\frac{I}{12}\right)^t y_0+\left[1+\left(1+\frac{I}{12}\right)+\left(1+\frac{I}{12}\right)^2+\cdots+\left(1+\frac{I}{12}\right)^{t-1}\right](-P)$

Now, there's an algebraic simplification of this, but instead of waving my hands and asking you to trust me -- that's a degree of trust maybe I haven't earned -- let's have Maple do it. After all, surely we can agree that a computer isn't likely to make an algebra mistake!

a video walkthrough of this

The command we're going to use is called rsolve.

First we need to tell Maple our finite difference model.
- For rsolve to work, we have to enter our unknown y in function notation, rather than writing yt or y_t or something like that.
- I've also called the variables rate and payment, both to make them easier to remember and because Maple treats the letter I as special so I can't use it.
Now, we could ask Maple to solve this for us:
- As with all solving commands, the first slot in the command is an equation (or system of equations), and the second slot is the unknown we're solving for.
Actually, since we know that 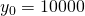$y_0=10000$ , when we invoke the rsolve command, we can just tell Maple that:
Now copy-and-paste the output from rsolve into a function called y:
We let Maple know that the rate is 6%:
And ask what the payment ought to be, if we want to pay off the loan in 24 months:
To find out, at a given monthly payment, how many months it takes to pay off the debt, we first specify the payment and then solve for t:

Thus we see that, at a payment of $150 each month it will take more than 81 months to pay off the full debt; to pay it off in 24 months will require quite a bit more -- $443.21!

One practical observation to make: if we take the 81 months to pay, we'll pay a bit more than $81\cdot 150=12150$ . If we make the greater payments, the total amount paid is $24\cdot443.21=10637.04$ (I've rounded to the next cent rather than the nearest cent because that's how payments work.)

So the question we'd have to ask ourselves is: is it worth the approximately $1,500 to have $300 more walking-around money on a monthly basis? If the $300 each month is the difference between having a babysitter or not, the answer may well be that we have no choice; if the extra $300 each month would go to partying, then maybe it is better to pay down our debt.

Variables in Maple

One thing to watch out for in Maple is that when you assign a value to a variable, it stays assigned. So in step 7, above, we assigned the value 150 to the variable payment. If we try to execute step 6 again, Maple gets cranky with us:

(Of course it does -- "solving for 150" is kind of an absurd request.) To avoid this hassle, let's clear out that value. There are two ways to do this.

There is a panel called Variables to the left of the main execution area. This lists all the variables that are currently defined. In our worksheet, we've defined finitediff, payment, rate, and y. To delete a variable, simply right-click (on a Mac, command-click) the name of the variable and select "Unassign".
The other way is to use the command unassign:

Takeaways/Deliverables

To say you've successfully completed this lesson, you should be able to do the following:

Derive a finite difference model for compound interest, given rate and initial investment.
Use Maple to solve your finite difference model.
Use Maple and your finite-difference model to find the required monthly payment to pay off a loan in a specified period of time.
Compute the total amount paid on a loan.

These skills are what you'll need to complete the WebAssign homework for this Lesson.