In Lesson 12-I, we considered predator-prey relationships. These were modeled by the Lotka-Volterra equations
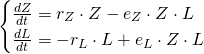
In this lesson, we'll refine the Lotka-Volterra model, and then we'll extend it to cover populations which interact in other ways than the predator-prey relationship.
A Better Model
Recall from Lesson 12-I that the first term (![]() ) of the prey equations came from the assumption of unrestricted growth. That is, we assumed that (in our example) the zebra had unlimited space, food, etc. But we know from Lesson 10 that this is not such a reasonable assumption. Even if there were no lions present, we'd expect the zebra population to encounter problems with running out of grazing space, for example. So the appropriate first term of
) of the prey equations came from the assumption of unrestricted growth. That is, we assumed that (in our example) the zebra had unlimited space, food, etc. But we know from Lesson 10 that this is not such a reasonable assumption. Even if there were no lions present, we'd expect the zebra population to encounter problems with running out of grazing space, for example. So the appropriate first term of ![]() might look more like
might look more like ![]() , where
, where ![]() is the carrying capacity (maximum supportable population) of zebra.
is the carrying capacity (maximum supportable population) of zebra.
Then our updated model looks like
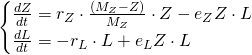
Let's see what Maple has to say. We'll use ![]() . Entering this all into Maple looks like:
. Entering this all into Maple looks like:

Then we can use dsolve and odeplot. Let's see what happens if we start out with 200 zebra (the carrying capacity, if there weren't any lions), and 50 lions:

The zebra rapidly decline, and the lions increase to a point, but then (running out of food) the lion population declines quickly. It looks like the zebra population is going to die off, too:

If we take a longer view, though, we see that the zebra population recovers enough to support a temporary spike in the lion population:

This phenomenon repeats, but each time it gets a little less dramatic:

. . . until eventually both populations settle into a nearly-constant state, around 75 zebra and 3 lions:

What does this look like if we plot the populations against each other? Let's run
[> odeplot(solution, [[Z(t), L(t)]], 60 .. 250, frames = 200)

The populations are spiraling into an equilibrium instead of orbiting around it like they did in Lesson 12-I. What's the equilibrium?
![]()
There are three: one representing no lions and no zebra, one representing a stable zebra population with no lions, and 75 zebra and about 3 lions.
Other Kinds of Interactions
Predatory-prey relationships are not the only kind of relationships that might hold between two interacting species. We could also have:
Mutualism
In this relationship, the two species would do fine on their own, but their interactions are mutually beneficial. If we assume each species has logistic growth, we get a system like
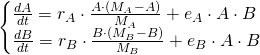
where ![]() are the natural growth rates of species A and B, respectively,
are the natural growth rates of species A and B, respectively, ![]() are their natural carrying capacities, and
are their natural carrying capacities, and ![]() and
and ![]() encode the (positive) effect that interactions between the two species have on each species.
encode the (positive) effect that interactions between the two species have on each species.
Symbiosis
In this relationship, the two species depend on each other -- they would die off without each other -- and their interactions are mutually beneficial. If we assume exponential decay without the other species, we get a system like
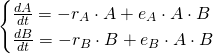
Commensalism
In this relationship, both species do fine on their own. One of them isn't impacted at all by the other, but the other benefits from the relationship. (Think of humans and urban pigeons: we don't get much out of the pigeons, but they get a lot out of us.) This results in a system like
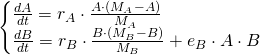
Competition
In this relationship, both species do fine on their own, but they negatively impact each other. This results in a system like
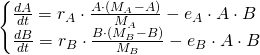
With each of these models, the important things to look at are:
- whether the natural term is logistic or exponential
- the sign (positive or negative) of the interaction term
Takeaways/Deliverables
To say you've successfully completed this lesson, you should be able to do the following:
- Use dsolve and odeplot to plot solutions of a modified Lotka-Volterra system against time.
- Use dsolve and odeplot to plot solutions of a modified Lotka-Volterra system against each other.
- Use solve to find equilibria of a modified Lotka-Volterra system.
- Identify which species relationships correspond to which modified Lotka-Volterra systems.
These skills are what you'll need to complete the WebAssign homework for this Lesson.