In Lesson 11, we considered three subpopulations within one larger population: the susceptibles, the infecteds, and the recovereds. We saw how the rate of change of each one of these populations related to the other populations, which gave a system of differential equations (which we then used Maple to understand solutions of).
What are some other populations whose rates of change depend on each other? One such relationship holds between predators and prey.
The Mathematical Model
Let's consider a pair of species, say zebra and lions. We'll try to model the population of these species over time, by making the following assumptions:
- There are unlimited resources (food, room, water, etc.) for the zebra; so in the absence of any lions, the zebra will exhibit uninhibited growth.
- The lions depend on the zebra as their main food source; so without any zebra, the lion population will exhibit uninhibited decline.
- Interactions between zebra and lions ('hunts') negatively impact the zebra population and positively impact the lion population.
- There are no other factors negatively impacting the zebra population, and no other factors positively impacting the lion population.
How do we turn this into a symbolic equation? Let's use ![]() and
and ![]()
According to assumption 4, there are two things to take into account when it comes to the rate of change of ![]() : the factors internal to the zebra population, and interactions with lions. That is,
: the factors internal to the zebra population, and interactions with lions. That is,
![]()
We saw in Lesson 8 that uninhibited growth should obey the exponential equation ![]() . We've seen in Lessons 10 and 11 that terms representing interactions between two populations look like the product of the two interacting populations. So we have:
. We've seen in Lessons 10 and 11 that terms representing interactions between two populations look like the product of the two interacting populations. So we have:
![]()
where ![]() is the natural growth rate of the zebra population and
is the natural growth rate of the zebra population and ![]() represents the impact that each hunt has on the zebra population.
represents the impact that each hunt has on the zebra population.
For the lion population, we have
![]()
To understand the first term, think about a world with no zebras and just lions. By assumption 2, lions mainly eat zebra. So in this situation, every day, some fraction of the lions would die of hunger. This looks very much like exponential growth, except instead of growth it's decay. So we have
![]()
(The interaction term is handled just the same way as before.) Here, ![]() is the natural decay rate of the lion population and
is the natural decay rate of the lion population and ![]() represents the impact each hunt has on the lion population.
represents the impact each hunt has on the lion population.
Putting it together, we have obtained the system of differential equations, known as the Lotka-Volterra equations:
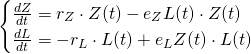
These equations are now known as the "Lotka-Volterra" model, after Alfred Lotka and Vito Volterra. Lotka was a chemist who derived the equations to study certain chemical reactions; Volterra was a mathematician who realized they could be used to study predator-prey systems.
Using Maple to "Solve" the Lotka-Volterra Equations
As with the SIR model, the Lotka-Volterra equations turn out not to have nice solutions. But we can use Maple to try and understand solutions.
First, let's have Maple draw a graph. Let's tell Maple about the Lotka-Volterra equations:

and pick some values for ![]() . Let's say the zebras are naturally growing at 10% per year and the lions are naturally declining at 75% per year (that's a very fast rate of decline, but then again we did take away their primary food source!):
. Let's say the zebras are naturally growing at 10% per year and the lions are naturally declining at 75% per year (that's a very fast rate of decline, but then again we did take away their primary food source!):

and pick some values for ![]() and
and ![]() :
:

Notice that this choice of values means the hunt has a bigger impact on the zebra population than it does on the lion population.
Let's see if Maple can tell us what the populations are, if we start out with 100 zebras and 10 lions:
[> dsolve({LotkaVolterra, lion(0) = 10, zebra(0) = 100})
It looks like the answer is: not really.
Plotting Both Populations Against Time
So we'll settle for using dsolve with numeric and odeplot:

This command plots the two populations (zebras in blue; lions in red) for the first ten years. The output shows:

So the zebra population declines (because of lions eating them); the lion population increases at first from eating so many zebras. But then there are fewer zebras, so the lion population decreases nearly to 0, which allows the zebra population to start increasing again.
If the lion population actually hit 0, we'd expect the zebra population to then grow according to ![]() , i.e. exponentially. So what happens later on? Let's extend the time window to 40 years:
, i.e. exponentially. So what happens later on? Let's extend the time window to 40 years:

After that dip around year 7, the zebra population bounces back. But more zebras means. . . more lions! So the lion population grows again, which means the zebra population decreases, so the lion population has to decrease, so the zebra population can increase, so. . .

We can see that this cycle will repeat about once every 25 years.
What if we change the number of lions and zebras, say by releasing 5 additional lions?![]()

Notice that the maximum zebra population is actually higher (130) than it was when we started with fewer lions. That's a bit surprising. The minimum zebra population is also lower, which makes sense.
What if we add a whole bunch of lions, say starting with 100 lions and 100 zebras?

Kind of funky.
Plotting the Populations Against Each Other
Instead of a graph with one axis as time and one axis as population (either of zebra or of lions), we can try to draw a plot whose axes are population of zebra and population of lions. This makes sense to do, because if you think about it, the number of zebra depends on the number of lions (and vice versa).
How do we do this? Using odeplot. Let's plot several solutions at the same time; to do this we'll need to name them all separately. My naming convention is LV(initialnumberofzebra)(initialnumberoflions):

Then call odeplot like this:

How is this plot related to the graphs we drew above? Try giving odeplot the option frames, like this:

frames generates an animation, which you can watch by right-clicking (control-clicking on a Mac) the plot and selecting Animation > Play:

As time plays in this animation, we're seeing the number of zebra (our horizontal position) and lions (our vertical position) change.
To put all four solutions together into one big plot, we call odeplot with each of them, giving each odeplot a name:
plot1 := odeplot(LV10010, [[zebra(t), lion(t), color = blue]], 0 .. 50) plot2 := odeplot(LV1010, [[zebra(t), lion(t), color = red]], 0 .. 50) plot3 := odeplot(LV10100, [[zebra(t), lion(t), color = black]], 0 .. 100) plot4 := odeplot(LV10020, [[zebra(t), lion(t), color = green]], 0 .. 50)
(I've also given each plot a different color. Notice that plot3 looks less smooth; this is because Maple is having a hard time approximating the solution.)
Now we combine all 4 plots into one single picture via:

You can see that the solutions all have roughly the same shape, but they are different sizes.
DEplot
Let's use our old friend DEplot again to clarify things. DEplot is from the DETools library, so we need to load that:
[> with(DETools)
Remember from Lesson 10 that DEplot requires us to tell it:
- a differential equation,
- what we're solving for,
- the range of the independent variable,
- the range of the dependent variable, and
- initial values
We want to solve for both ![]() and
and ![]() , or as Maple knows them, "zebra(t)" and "lion(t)". So our variable is actually represented in Maple as the pair
, or as Maple knows them, "zebra(t)" and "lion(t)". So our variable is actually represented in Maple as the pair
[zebra(t),lion(t)]
We need to represent the Lotka-Volterra equations this way, too; here's how you do that:
[> LV := [LotkaVolterra[1], LotkaVolterra[2]]
Let's plot the solution for the first 30 years, with zebra populations between 0 and 150, lion populations between 0 and 30, and the initial condition of 100 zebra and 10 lions:
[> DEplot(LV, [zebra(t), lion(t)], t = 0 .. 30, zebra = 0 .. 150, lion = 0 .. 30, [[zebra(0) = 100, lion(0) = 10]])
This should yield the following plot:
which shows the slope field and our solution in yellow. We can add other solutions, too:
As in Lesson 10, DEplot give us a good idea of what's going on: the populations are cycling counterclockwise around some central point, which looks to be at around 75 zebra and 5 lions.
Equilibria
In Lesson 10, we discussed equilibria: that is, solutions which were really just constants. Here an equilibrium means both populations are constant. Where are the equilibria? We need to solve the system of algebraic equations
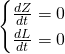
which Maple can do easily:
![]()
There are two equilibria: 0 zebra and 0 lions; and 75 zebra and 5 lions. This makes sense: if there aren't any animals at all, that condition will persist indefinitely; and if there are exactly 75 zebra and 5 lions, the populations are in precise balance.
Takeaways/Deliverables
To say you've successfully completed this lesson, you should be able to do the following:
- Use dsolve and odeplot to plot solutions of a Lotka-Volterra system against time.
- Use dsolve and odeplot to plot solutions of a Lotka-Volterra system against each other.
- Use DEplot to draw a slope field for a Lotka-Volterra system.
- Use solve to find equilibria of a Lotka-Volterra system.
These skills are what you'll need to complete the WebAssign homework for this Lesson.