In Lesson 1, we considered the problem of maximizing profit in the context of declining market price. We solved this problem by finding where the derivative of the profit function was zero. In Lesson 3, we saw that if there are two markets, the profit is a function of two variables, which puts it beyond the scope of your single-variable calculus course.
Let's see how to use Maple to find the minimum and maximum values of a function of two variables.
The Mathematical Model
Let's consider the problem of selling steel barrels in the US and Canada. Thanks to the North American Free Trade Agreement, we'll centralize production at a facility in Sarnia, Ontario, and ship barrels into the US without any trouble. We'll work in US dollars throughout.
Our fixed costs are $10,000, and each of our barrels costs $3.50 to produce. Our market research tells us that, initially, the market price per steel barrel in the US is $97, and the market price per steel barrel in Canada is $85.
As in Lesson 1, we expect that selling barrels in the US will drop the market price in the US; for this example let's say that drop is $0.10 per barrel sold. Similarly, we expect that selling barrels in Canada will drop the market price in Canada; let's say that drop is $0.07 per barrel sold.
Again, thanks to NAFTA, the two markets do interact. So each barrel sold in the US will drop the Canadian market price, and each barrel sold in Canada will drop the US market price. Let's organize all this information into a table:
| market | initial market price | price response in Canada | price response in US |
| Canada | $85 | -$0.07 per b. sold in Canada | -$0.02 per b. sold in Canada |
| US | $97 | -$.01 per b. sold in the US | -$0.10 per b. sold in the US |
Our goal will be to maximize profit. Recall that
![]()
so we should first derive symbolic expressions for revenue and cost.
screencast: using Maple to translate these word equations into symbolic equations
Let's use the following symbols:
| symbol | |||||
| meaning | barrels sold in Canada | barrels sold in US | profit | costs | revenue |
| units | barrels | barrels | $ | $ | $ |
Then we can set up the following description of the prices in each market:
![Rendered by QuickLaTeX.com [price\ in\ Canada] = 85-.07x-.02y\\ [price\ in\ US] = 97-.01x-.10y](https://ma132.wordpress.ncsu.edu/wp-content/ql-cache/quicklatex.com-fe6ca9c4fee80957344d8b30024ac183_l3.png)
Then the revenue generated in Canada is
![]()
and the revenue generated in the US is
![]()
The total revenue is just the sum of these, so we have
![]()
What about costs? Recall that
![]()
The number of units we've produced is ![]() ; our fixed costs are $10,000; and each barrel costs $3.50 to produce. So we have
; our fixed costs are $10,000; and each barrel costs $3.50 to produce. So we have
![]()
Thus we can translate the word equation ![]() into the symbolic equation
into the symbolic equation
![]()
or in simplified form,
![]()
Now that we have our profit function, we can try to find the production levels -- that is, the values of ![]() and
and ![]() -- which maximize it.
-- which maximize it.
Using Maple to Optimize
Plotting in Two Variables
screencast: plotting a function of two variables
To plot a function of two variables, we'll need 3 dimensions: two for the inputs, and one for the output. We'll need to load the conspiratorial-sounding package plots:
[> with(plots)
Now, let's try to plot the function ![]() . If you followed the screencast above, it will already be in your Maple sheet; otherwise you'll need to define:
. If you followed the screencast above, it will already be in your Maple sheet; otherwise you'll need to define:
[> P(x,y):=81.5*x-0.07*x^2-0.03*x*y+93.5*y-.10*y^2-10000
Now let's plot. Because this will be a three-dimensional plot, we'll use the command plot3d:

Just like plot, plot3d requires us to specify the range of values for the variables. Here I've looked at sales values between 0 and 1200 in each market. Notice that for some sales levels, the profits are quite negative. Also notice that our view of certain parts of the graph is obstructed by the graph itself, so it's hard to eyeball where the maximum profit occurs (somewhere around ![]() and
and ![]() , maybe?
, maybe?
In Maple, you can change the perspective by clicking and dragging the graph. But that only goes so far. Here's another way to visualize the profit function:
[> contourplot(P(x,y),x=0..1200,y=0.1200,filledregions)

This is what's called a shaded contour plot, and it uses color to indicate the values of the profit function (blue is higher profit; red is lower profit). Let's focus more closely to see if we can isolate the maximum of the profit function. The big blue region extends for ![]() between about 100 and about 900, and
between about 100 and about 900, and ![]() between about 25 and about 700, so we'll zoom in just on that:
between about 25 and about 700, so we'll zoom in just on that:
Now we can see, in a lot finer detail, that the maximum is somewhere in this new blue region. Let's zoom in again:

So now we've narrowed down the maximum profit to occur someplace with ![]() and
and ![]() . A decent guess would be right in the middle of this blue region:
. A decent guess would be right in the middle of this blue region: ![]() ,
, ![]() .
.
Derivatives of Functions of Two Variables
As in Lesson 1, the just-eyeball-it method leaves a lot to be desired, in some philosophical sense. We'd like an analytical solution that will yield a non-guesswork solution.
a screencast of this part of the Lesson
Since ![]() is a function of two variables, it actually has two kinds of derivatives: one where we think of
is a function of two variables, it actually has two kinds of derivatives: one where we think of ![]() as a function of
as a function of ![]() and differentiate in
and differentiate in ![]() , and one where we think of
, and one where we think of ![]() as a function of
as a function of ![]() and differentiate in y. We refer to these as the partial derivatives of
and differentiate in y. We refer to these as the partial derivatives of ![]() , because each one accounts for only some of the variation in
, because each one accounts for only some of the variation in ![]() . The symbol for a partial derivative is:
. The symbol for a partial derivative is:
![Rendered by QuickLaTeX.com \frac{\partial P}{\partial x} = [derivative\ of\ P\ with\ respect\ to\ x]\\\frac{\partial P}{\partial y} = [derivative\ of\ P\ with\ respect\ to\ y]](https://ma132.wordpress.ncsu.edu/wp-content/ql-cache/quicklatex.com-b50b547a7f01832f981a3e9229964319_l3.png)
Luckily for us, Maple treats partial derivatives just like ordinary derivatives:

which is the Maple way of saying that
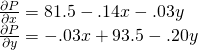
As in the case of just one variable, at a maximum of ![]() , the derivative should be zero. But here, that means we should have both partial derivatives equal to zero. So we need to solve the system of equations
, the derivative should be zero. But here, that means we should have both partial derivatives equal to zero. So we need to solve the system of equations
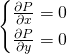
Again luckily for us, Maple is very good at that: the command
[> solve({diff(P(x,y),x)=0,diff(P(x,y),y)=0})
is the Maple version of this request.
![]()
So our initial guess of ![]() ,
, ![]() was off but not by too much. To optimize our profit, we should try to produce 891 barrels in Sarnia, of which we'll sell 498 in Canada and 393 in the US. (I've rounded to the nearest barrel, because it's hard to split a barrel.) The profit we'll turn from this will be $28655.90:
was off but not by too much. To optimize our profit, we should try to produce 891 barrels in Sarnia, of which we'll sell 498 in Canada and 393 in the US. (I've rounded to the nearest barrel, because it's hard to split a barrel.) The profit we'll turn from this will be $28655.90:
![]()
Takeaways/Deliverables
To say you've successfully completed this lesson, you should be able to do the following:
- Define functions in Maple using function notation.
- Visualize a function of two variables using Maple's plot3d and contourplot commands.
- Use Maple to take partial derivatives.
- Solve a system of algebraic equations using Maple's solve command.
- Use the above skills to optimize a function of two variables.
These skills are what you'll need to complete the WebAssign homework for this Lesson.