What is Maple?

Maple is a computer algebra system. (Other CASes you may have heard of are Mathematica and Matlab.) That means it's able to do symbolic computations, of the kind you learned to do in your math classes. You could think of it as a graphing calculator on steroids.

Starting up Maple

When you open Maple, you're met with this screen, which gives you lots of options. The options on the right give you an idea of the sorts of things that Maple can do.

We will want to open a New Worksheet:

Clicking on New Worksheet takes you to a prompt that looks like this:

Maple Is a Calculator

The first thing we'll have Maple do is just some arithmetic. Type

[> 3*7^3

and hit Enter. You'll see:

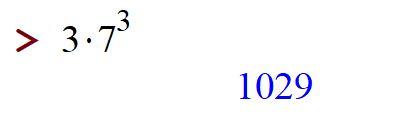
As you type, Maple converts your typing into pretty math: the asterisk * becomes a dot; the caret ^ becomes a power. Everything you type appears in black. Everything Maple says appears in blue.

Maple Knows Algebra

Maple knows how to do a lot of algebra; for example, it can solve equations:

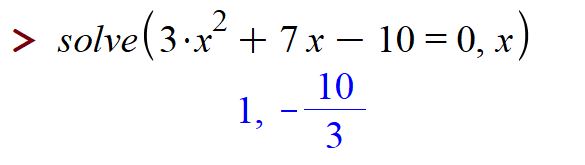
and factor polynomials:

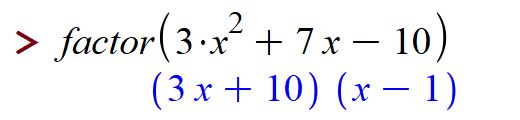
Maple can also do algebra with more than one variable, for example:

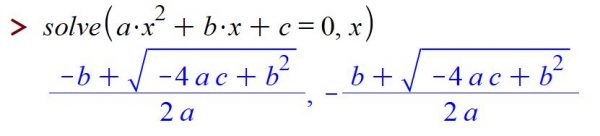
And Maple can solve systems:

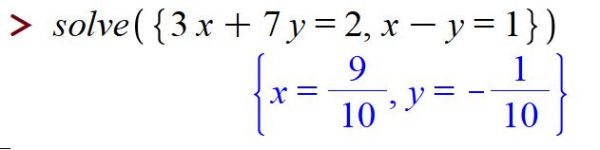
Definitions in Maple

One of the most powerful things about Maple is its ability to remember the results of computations. Basically anything can be named and saved. For example, if we wanted to solve a general quadratic equation, we could use

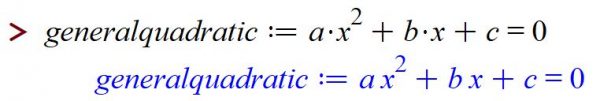
which tells Maple that the equation $ax^2+bx+c=0$ is something we'll be calling generalquadratic. Then we can refer to generalquadratic by name, say when we involve solve:

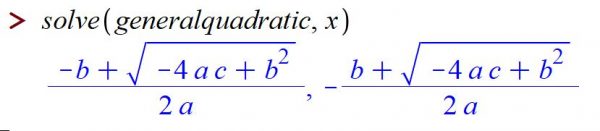
By the way, we can also solve for other variables, say $c$ instead of $x$ :

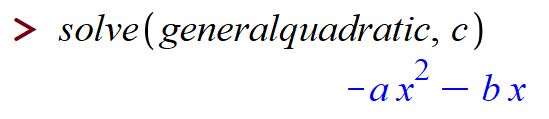
Observe that when we define something, we need to use colon-equals := rather than just =.

If we define values for $a$ and $c$ then Maple will use those:

Maple Can Graph

Now let's try to draw a graph. To do this, we need everything to concrete -- no variables except the one we want to graph in. So:

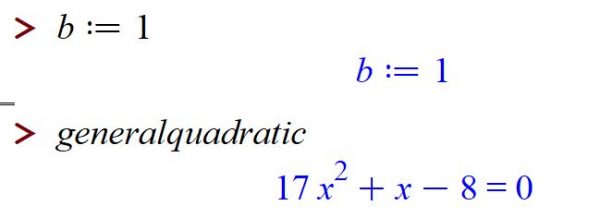
The command to draw a graph is plot:

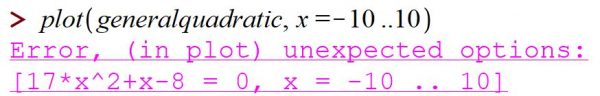
What happened? We tried to plot generalquadratic, which is the equation

$17x^2+x-8=0$

But that's nonsense. (A nice thing about Maple is that when it encounters an error, it tells you something about the nature of the error, or at least where the error happened.

What we meant was to plot the function

$f(x)= 17x^2+x-8$ ,

which occurs as the left-hand side of generalquadratic. Maple knows about left-hand sides and right-hand sides:

That's better.

Maple Knows Calculus

We'll spend a lot of time exploring Maple's calculus abilities, but for now we can demonstrate the basic two calculus skills:

Differentiation: Maple tells us that $\frac{d}{dx}\sin(x^2+7x)=(2x+7)\cos(x^2+7x)$

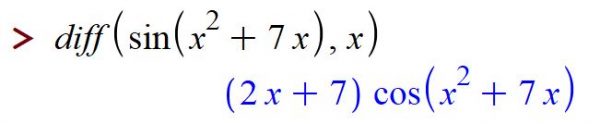
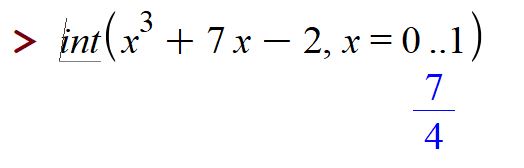
Integration: Maple tells us that $\displaystyle\int_0^1 x^3+7x-2\ dx=\frac{7}{4}$

**What Can't Maple Do?**

Maple can't read your mind. In some ways, computers are very very dumb. They will do exactly what you tell them to do. If you tell them to do nonsense, they will dutifully try to do nonsense.

But if you ask Maple to perform basically any mathematical computation, and you ask it in a way that it understands, you'll be surprised at powerful it is.