In Lesson 8, we saw that there is good theoretical reason to expect populations to grow according to exponential functions. (Actually, we'll see later that the reality is a good deal more subtle, but for now let's roll with it.) But the real world is a messy: we have measurement error, rounding error, probably our assumptions aren't exactly borne out in reality, etc.
Given that, we don't expect any exponential function to fit real-world data exactly. But we can ask, given real-world data we suspect of being exponential:
- Are the data really exponential?
- If so, what's the best-fitting exponential function to match the data?
The Mathematical Methods
The mathematical problem we need to solve is: given a bunch of data points (say, like the populations of Raleigh and Wake County:)
| year | Raleigh | Wake County |
| 1900 | 13643 | 54626 |
| 1910 | 19218 | 63229 |
| 1920 | 24418 | 75155 |
| 1930 | 37379 | 94757 |
| 1940 | 46879 | 109544 |
| 1950 | 65679 | 136450 |
| 1960 | 93931 | 169082 |
| 1970 | 122830 | 228453 |
| 1980 | 150255 | 301327 |
Which function of the form ![]() best matches the data?
best matches the data?
This is actually a very similar problem to Lesson 2, where we asked, Which linear function best matches the data? As in that case, Excel provides a ready-made solution for us to use, called the trendline. To use this feature, we simply:
- Enter the data in Excel. We'll work with Raleigh's population. To make things just a bit simpler, let's change time to count "years since 1900":

- Plot the data on a scatter plot and select one of the data points:

- Right-click (control-click on a Mac) and "add trendline...".
- In the Trendline Panel, we see that there are several options. By default, "linear" is selected; for these data, the linear model looks okay but not great. To quantify this, select "display R-squared".

- Now select "exponential", and you'll see how much better the curve fits, and how much closer to 1 the value of
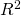 has become.
has become.

- Click "display equation on chart" to get Excel to report the values of
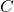 and
and  that it thinks are best. In this case, it's
that it thinks are best. In this case, it's 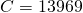 and
and 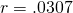 .
. - We should translate back into our language: our exponential model here is
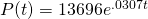 .
.
The Log-Transform Trick (Excel)
That was a bit messy, and as you can see, there's not much hope we could have done it by hand. There's another approach, too.
This relies on a function called the natural logarithm, which whatever else it does, has the following three nice properties:
![]() "The log of a product is the sum of the logs."
"The log of a product is the sum of the logs."
![]() "Natural log undoes the exponential."
"Natural log undoes the exponential."
![]() "Exponential undoes natural log."
"Exponential undoes natural log."
To carry out the log-transform fitting:
- Make a table in Excel which contains the data we want to fit, and also the log-transformed data:

- Plot the log-transformed data. :

- Get a (linear) trendline for the log-transformed data:

The trendline is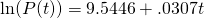
- Use the trendline for the log-transformed data as a power for
 :
:
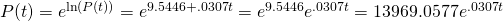
- This is the exponential model.
The log-transform trick allows us to use linear techniques (which are computationally easier) and to use our eyes (which are good at seeing lines) to find exponential models when they're appropriate. Observe that we have the following correspondence between the parameters
| log-transformed fit | slope m | intercept b |
| untransformed fit | growth rate |
initial population |
Now, try both techniques (Excel's exponential fit and the log-transform-and-linear-fit approach) to find the growth rate of Wake County's population 1900 -- 1980.
Takeaways/Deliverables
To say you've successfully completed this lesson, you should be able to do the following:
- Use Excel to generate a scatter plot from given data.
- Use Excel to plot a best-fit exponential and report its equation.
- Use Excel to compute the sum-of-squares measure to see how well a given exponential model fits given data, and to compare how well an exponential model fits as opposed to a linear model.
- Use the log-transform trick and Excel's trendline to find an exponential model.